HELP DOCUMENTS
|
|
|
GUIDELINES FOR mathFISH
This document provides guidelines for using mathFISH on a tool by tool basis. An example is provided for the usage of each tool.
This tool calculates all modeled thermodynamic properties of a single probe for any target molecule provided (i.e., perfect match or with mismatches). The output includes free energy values (ΔGo1, ΔGo2, ΔGo3, ΔGooverall), hybridization efficiency, and the formamide dissociation profile.
Input
-
Enter hybridization conditions: Temperature, Na+ concentration, and probe concentration.
-
Note: the probe concentration does not affect free energy values but affects hybridization efficiency and formamide curve.
-
-
Enter probe sequence information using one of the three options (check circle and enter value):
-
Option 1: Position of nucleotides at the 5’ and 3’ ends of target site (according to the numbering of entered sequence). In general, these positions can be easily obtained from alignment software used for probe design (e.g. Bioedit, ARB ...).
-
This option cannot be used for mismatched targets since mismatch information is not delivered.
-
Option 2: Probe sequence from 5’ to 3’ end. In this option, mathFISH will align the probe with the target to determine the best matching target site.
-
This is the only option for mismatched targets.
-
Option 3: Target site sequence (can use T instead of U; all T’s in target sequence will be converted to U’s) from 5’ to 3’. If the target site is available on the screen interface of the alignment software (e.g. Bioedit, ARB ...) this option can be used simply by copying and pasting.
-
This option cannot be used for mismatched targets as the exact target site will not be present in the target sequence.
-
Note also that this is the reverse complement of probe sequence and vice versa.
-
Note: Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the probe sequence. For probes with degeneracy, evaluate the different combinations separately.
-
-
Enter target sequence information.
-
Select the target molecule.
-
If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is. This is important for the calculation of ΔGo3.
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for the alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
Enter target sequence (can use T instead of U; all T’s in target sequence will be converted to U’s) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive). Gaps are removed by mathFISH.
-
Note: Degeneracy in target sequence (e.g. N, indicating all possibilities, i.e. A, C, G, or T) is treated as a mismatch at the probe target site. Other degeneracies in the target sequence are not allowed to base-pair, and this may affect the accuracy of ΔGo3 values.
-
Output
-
Probe-target site alignment: This is a text output that shows the user how the probe aligns with the target site and how many mismatches there are.
-
Tabular list of thermodynamic values: This list includes the free energy values (ΔGo1, ΔGo2, ΔGo3, ΔGooverall), hybridization efficiency, and the melting formamide point ([FA]m).
-
Graphical display of hybridization efficiency: The calculated hybridization efficiency value is indicated on a plot of hybridization efficiency as a function of ΔGooverall. Note the following:
-
The position of the sigmoid curve representing the relationship between hybridization efficiency and ΔGooverall is dependent on probe concentration. It will shift right at higher concentrations.
-
Based on a color coding, the sigmoid curve provides a recommended guideline for the optimization of sensitivity and specificity for perfect matches only. Here are the color coded recommendations:
-
Green: Recommended ΔGooverall range due to low risk for both false negatives and false positives.
-
Orange: Theoretical optimal for avoiding false positives, but with an increased risk of false negative.
-
Red: Strongly recommended against due to high risk of false negative.
-
Yellow: Very low risk of false negative, but increased risk of false positive due to excessive probe affinity.
-
-
Graphical display of formamide dissociation profile: This is the plot of hybridization efficiency as a function of formamide concentration.
-
The whole output can be downloaded as a report in text format.
Example
Take probe GAM42a, a probe that targets gammaproteobacteria. This probe targets positions 1027-1043 on the 23S rRNA (in E. coli numbering). Let the example target be the 23S rRNA sequence of E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), which is a perfect match to this example probe. The objective is to evaluate the thermodynamics of the hybridization of GAM42a with E. coli.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH), and probe concentration to 500nM (in the general range which is 250-1000nM).
-
Select probe sequence entry and then enter “GCCTTCCCACATCGTTT” in the probe sequence box.
-
Select target molecule as "Large Subunit rRNA" and domain of target organism as "Bacteria".
-
Enter target sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output:
-
The probe-target alignment result is shown below. It indicates a perfect match alignment.
Figure 1. Alignment of GAM42a with perfect match target.
..........................PROBE--5'TTTGCTACACCCTTCCG3'
.........|||||||||||||||||
TARGET-3'AAACGATGTGGGAAGGC5'
..........................
Table 1. Thermodynamic descriptors of GAM42a with perfect match target
| ΔGo1 | -21.0 kcal/mol |
| ΔGo2 | 1.5 kcal/mol |
| ΔGo3 | -5.5 kcal/mol |
| ΔGooverall | -15.4 kcal/mol |
| [FA]m* | 37.6 % |
| Hybridization Efficiency** | 0.9999 |
* Melting formamide concentration
** At 0% formamide
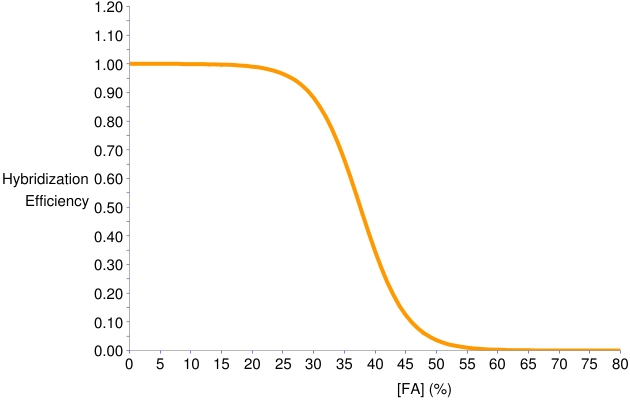
- The hybridization efficiency value is marked on the hybridization efficiency – ΔGooverall curve as shown below. This indicates a perfect design value since probe is close the beginning of the plateau (see also Recommendations).
Figure 2. Hybridization efficiency of GAM42a

- The formamide curve is shown below. This predicts that formamide concentrations 25-40% provide high stringency where probe-target duplex melts.
Figure 3. Predicted formamide dissociation profile of GAM42a
-
The same results would be obtained if:
-
Target site position was selected as probe entry with positions 1027 (5’) and 1043 (3’) which are according to the sequence used.
-
Target site entry was selected and “AAACGATGTGGGAAGGC” (reverse complement of probe) was entered.
-
The target sequence was entered in plain text.
-
-
If, instead of the perfect matching target E. coli O157:H7 str. Sakai, the one mismatch non-target organism Nitrosomonas europaea ATCC 19718 (NC_004757) was used (click here for sequence), the alignment and tabulated results would look as shown below. Note the following:
-
In this case, target site entry options will not work. Probe sequence entry option must be used.
-
The mismatch is indicated in probe alignment.
-
The hybridization efficiency is still in the recommended zone, indicating potential cross hybridization problems since this is a mismatch organism.
-
For a more sophisticated analysis of mismatch effect, see Mismatch Analysis tool.
-
Figure 4. Alignment of GAM42a with one-mismatch non-target.
...............A..........PROBE--5'TTTGCT.CACCCTTCCG3'
.........||||||.||||||||||
TARGET-3'AAACGA.GTGGGAAGGC5'
...............A..........
Table 2. Thermodynamic descriptors of GAM42a with one-mismatch non-target.
| ΔGo1 | -18.0 kcal/mol |
| ΔGo2 | 1.5 kcal/mol |
| ΔGo3 | -2.8 kcal/mol |
| ΔGooverall | -15.2 kcal/mol |
| [FA]m* | 30.1 % |
| Hybridization Efficiency** | 0.9999 |
* Melting formamide concentration
** At 0% formamide
This tool calculates ΔGooverall values for a series of probes of uniform length that span a target frame on the targeted gene. In other words, the user defines a window on the target sequence and the tool walks an oligomer of user-defined length over this window, to calculate the ΔGooverall value at each position.
Input
-
Enter hybridization conditions: Temperature and Na+ concentration.
-
Enter target frame and probe information.
-
Position of nucleotides at the 5’ and 3’ ends of the target frame (according to the numbering of entered sequence).
-
Probe length.
-
Note: The total number of probes (p) to be walked over the defined target frame is defined by p = (3’end position number) - (Probe Length) - (5’end position number) + 2. Currently, this number is not allowed to be greater than 20.
-
-
Enter target sequence information.
-
Select the target molecule.
-
If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is. This is important for the calculation of ΔGo3.
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
Enter target sequence (can use T instead of U; all T’s in target sequence will be converted to U’s during free energy calculations) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Note: Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the targeted frame. Other degeneracies in the target sequence are not allowed to base-pair, and this may affect the accuracy of ΔGo3 values.
-
-
Output
-
The graphical output is a plot of ΔGooverall series against the target site location as indicated by the 5’ end.
-
The data points of this plot can be downloaded as text or excel files.
Example
Take the 23S rRNA sequence of E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), which is a perfect match to the FISH probe GAM42a. Suppose that you are investigating the variation of probe affinity within the vicinity of the GAM42a target site.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH).
-
Select target frame from position 1017 to 1052, i.e. enter these numbers in the 5’ and 3’ end boxes in the respective order.
-
Note that this frame contains the target site of GAM42a, 1027-1043.
-
-
Enter probe length as 17 nucleotides (this matches the length of GAM42a).
-
Select "Large Subunit rRNA" as target molecule and "Bacteria" as domain of target organism.
-
Enter target sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output:
- The ΔGooverall series plot is as shown below. The data points represent 1052-17-1017+2=20 probes walked over the target frame.
Figure 5. ΔGooverall series for 17-nt long probes targeting positions 1017 to 1036 in E. coli 23S rRNA
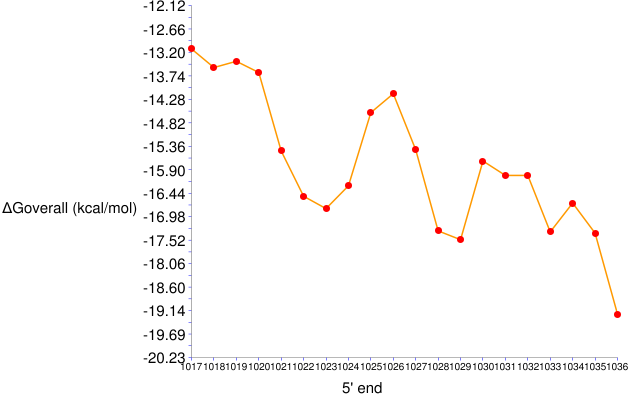
- The target site of GAM42a is represented by 1027 on the x-axis. The ΔGooverall value of this probe is around -15.4 kcal/mol, the same result as in the General Analysis example.
This tool calculates ΔGo1 values for a series of probes of uniform length that span a given target frame on the targeted gene. In other words, the user defines a window on the target sequence and the tool walks an oligomer of user-defined length over this window, to calculate the ΔGo1 value at each position.
Input
-
Enter hybridization conditions: Temperature and Na+ concentration.
-
Enter target frame and probe information.
-
Position of nucleotides at the 5’ and 3’ ends of the target frame (according to the numbering of entered sequence).
-
Probe length.
-
Note: The total number of probes (p) to be walked over the defined target frame is defined by p = (3’end position number) - (Probe Length) - (5’end position number) + 2. Currently, this number is not allowed to be greater than 50.
-
-
Enter target sequence information.
-
Enter target sequence (can use T instead of U; all T’s in target sequence will be converted to U’s during free energy calculations) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Note: Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the targeted frame (degeneracy elsewhere is immaterial). For sequences with degeneracy, evaluate the different combinations separately.
-
-
Output
-
The graphical output is a plot of ΔGo1 series against the target site location as indicated by the 5’ end.
-
The data points of this plot can be downloaded as text or excel files.
Example
Take the 23S rRNA sequence of E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), which is a perfect match to the FISH probe GAM42a. Suppose that you are investigating the variation of ΔGo1 within the vicinity of the GAM42a target site.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH).
-
Select target frame from position 1017 to 1052, i.e. enter these numbers in the 5’ and 3’ end boxes in the respective order.
-
Note that this frame contains the target site of GAM42a, 1027-1043.
-
-
Enter probe length as 17 nucleotides (this matches the length of GAM42a).
-
Enter target sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output:
- The ΔGo1 series plot is as shown below. The data points represent 1052-17-1017+2=20 probes walked over the target frame.
Figure 6. ΔGo1 series for 17-nt long probes targeting positions 1017 to 1036 in E. coli 23S rRNA
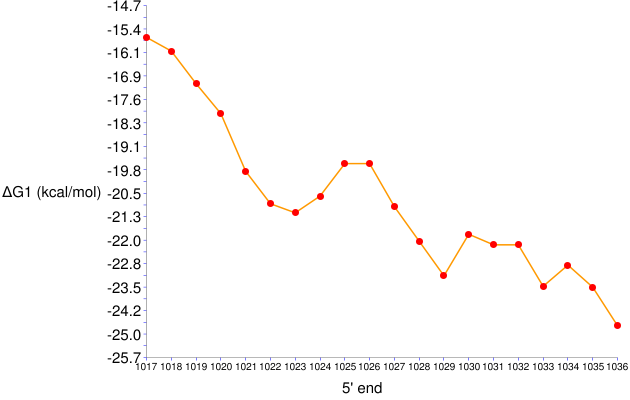
- The target site of GAM42a is represented by 1027 on the x-axis. The ΔGo1 value of this probe is around -21 kcal/mol, the same result as in the General Analysis example .
This tool calculates ΔGo2 values for a series of probes of uniform length that span a given target frame on the targeted gene. In other words, the user defines a window on the target sequence and the tool walks an oligomer of user-defined length over this window, to calculate the ΔGo2 value at each position.
Input
-
Enter hybridization conditions: Temperature and Na+ concentration.
-
Enter target frame and probe information.
-
Position of nucleotides at the 5’ and 3’ ends of the target frame (according to the numbering of entered sequence).
-
Probe length.
-
Note: The total number of probes (p) to be walked over the defined target frame is defined by p = (3’end position number) - (Probe Length) - (5’end position number) + 2. Currently, this number is not allowed to be greater than 50.
-
-
Enter target sequence information.
-
Enter target sequence (can use T instead of U; all T’s in target sequence will be converted to U’s during free energy calculations) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Output
-
The graphical output is a plot of ΔGo2 series against the target site location as indicated by the 5’ end.
-
The data points of this plot can be downloaded as text or excel files.
Example
Take the 23S rRNA sequence of E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), which is a perfect match to the FISH probe GAM42a. Suppose that you are investigating the variation of ΔGo2 within the vicinity of the GAM42a target site.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH).
-
Select target frame from position 1017 to 1052, i.e. enter these numbers in the 5’ and 3’ end boxes in the respective order.
-
Note that this frame contains the target site of GAM42a, 1027-1043.
-
-
Enter probe length as 17 nucleotides (this matches the length of GAM42a).
-
Enter target sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output.
- The ΔGo2 series plot is as shown below. The data points represent 1052-17-1017+2=20 probes walked over the target frame.
Figure 7. ΔGo2 series for 17-nt long probes targeting positions 1017 to 1036 in E. coli 23S rRNA
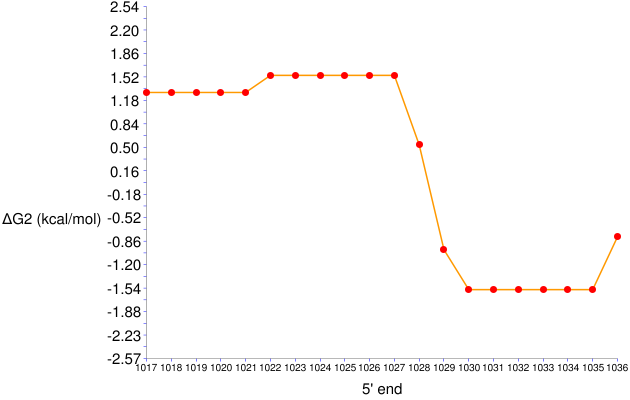
- The target site of GAM42a is represented by 1027 on the x-axis. The ΔGo2 value of this probe is around 1.5 kcal/mol, the same result as in the General Analysis example.
This tool calculates ΔGo3 values for a series of probes of uniform length that span a given target frame on the targeted gene. In other words, the user defines a window on the target sequence and the tool walks an oligomer of user-defined length over this window, to calculate the ΔGo3 value at each position.
Input
-
Enter hybridization conditions: Temperature only.
-
Note: Corrections for Na+ concentration is not available for ΔGo3 calculations. Therefore, the value of 1M, the concentration at which RNA folding rules were originally obtained, is used as a first approximation.
-
-
Enter target frame and probe information.
-
Position of nucleotides at the 5’ and 3’ ends of the target frame (according to the numbering of entered sequence).
-
Probe length.
-
Note: The total number of probes (p) to be walked over the defined target frame is defined by p = (3’end position number) - (Probe Length) - (5’end position number) + 2. Currently, this number is not allowed to be greater than 20.
-
-
Enter target sequence information.
-
Select the target molecule.
-
If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is (see below).
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
Enter target sequence (can use T instead of U; all T’s in target sequence will be converted to U’s during free energy calculations) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Output
-
The graphical output is a plot of ΔGo3 series against the target site location as indicated by the 5’ end.
-
The data points of this plot can be downloaded as text or excel files.
Example
Take the 23S rRNA sequence of E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), which is a perfect match to the FISH probe GAM42a. Suppose that you are investigating the variation of ΔGo3 within the vicinity of the GAM42a target site.
Input:
-
Use default temperature (T = 46oC).
-
Select target frame from position 1017 to 1052, i.e. enter these numbers in the 5’ and 3’ end boxes in the respective order.
-
Note that this frame contains the target site of GAM42a, 1027-1043.
-
-
Enter probe length as 17 nucleotides (this matches the length of GAM42a).
-
Select "Large Subunit rRNA" as target molecule and "Bacteria" as domain of target organism.
-
Enter target sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output:
- The ΔGo3 series plot is as shown below. The data points represent 1052-17-1017+2=20 probes walked over the target frame.
Figure 8. ΔGo3 series for 17-nt long probes targeting positions 1017 to 1036 in E. coli 23S rRNA
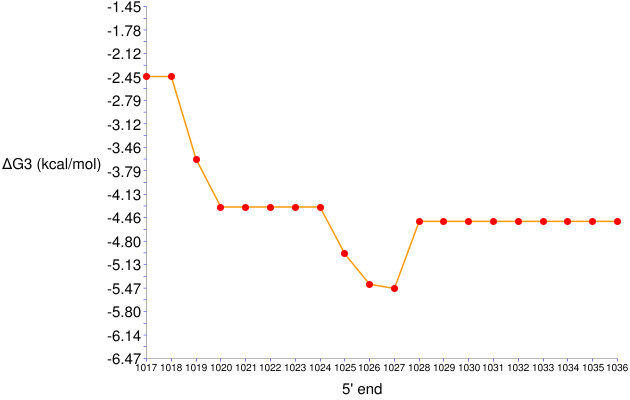
- The target site of GAM42a is represented by 1027 on the x-axis. The ΔGo3 value of this probe is around -5.5 kcal/mol, the same result as in the General Analysis example.
Formamide Curve Generator
This tool derives formamide dissociation profiles for up to 5 probe-target pairs. Mismatches are allowed in the target sequence.
Input
-
Enter hybridization conditions: Temperature, Na+ concentration, and probe concentration.
-
Enter target information.
-
Select the target molecule.
-
If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is. This is important for the calculation of ΔGo3.
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
-
Add probe-target pairs to the batch of analysis, one by one. For each additional pair, check the activation box (i.e., “Select” box) and enter probe and target sequences from 5’ to 3’.
-
Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the probe sequence. For probes with degeneracy, evaluate the different combinations separately.
-
Can use T instead of U in the target sequence (all T’s in target sequence will be converted to U’s). Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Note: Degeneracy in target sequence (e.g. N, indicating all possibilities, i.e. A, C, G, or T) is treated as a mismatch at the probe target site. Other degeneracies in the target sequence are not allowed to base-pair, and this may affect the accuracy of ΔGo3 values.
-
Output
-
Probe-target site alignment for all probe-target pairs: This is a text output that shows the user how the probes align with the target site and how many mismatches there are.
-
The graphical display of formamide dissociation profiles for all probe-target pairs, in the same plot.
-
The data points of this plot can be downloaded as text or excel files.
Example
Take probes GAM42a and BET42a, which target 23S rRNA of gammaproteobacteria and betaproteobacteria, respectively. Take two example targets: gammaproteobacterium E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695), and betaproteobacterium N. europaea ATCC 19718 (NC_004757). The objective is to compare the formamide dissociation profiles for all four probe-target combinations in this set.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH), and probe concentration to 500nM (in the general range which is 250-1000nM).
-
Select "Large Subunit rRNA" as target molecule and "Bacteria" as domain of target organism.
-
Check the first activation (“Select”) box.
-
Enter GAM42a sequence: “GCCTTCCCACATCGTTT”.
-
Enter E. coli O157:H7 str. Sakai 23S rRNA sequence (click here for acceptable formats; plain text would also work).
-
-
Check the second activation (“Select”) box.
-
Enter GAM42a sequence: “GCCTTCCCACATCGTTT”.
-
Enter N. europaea ATCC 19718 23S rRNA sequence (click here for acceptable formats; plain text would also work).
-
-
Check the third activation (“Select”) box.
-
Enter BET42a sequence: “GCCTTCCCACTTCGTTT”.
-
Enter E. coli O157:H7 str. Sakai 23S rRNA sequence (click here for acceptable formats; plain text would also work).
-
-
Check the fourth activation (“Select”) box.
-
Enter BET42a sequence: “GCCTTCCCACTTCGTTT”.
-
Enter N. europaea ATCC 19718 23S rRNA sequence (click here for acceptable formats; plain text would also work).
-
· Press SUBMIT button.
Output:
- The probe-target alignment results are shown below. The order of results follow from the order of entry. The alignments indicate that GAM42a and BET42a perfectly match E. coli and N. europaea, respectively, and both have a single mismatch to the other sequence.
PROBE ALIGNMENT :
Probe - Target Sequence 1
..........................
PROBE--5'TTTGCTACACCCTTCCG3'
.........|||||||||||||||||
TARGET-3'AAACGATGTGGGAAGGC5'
..........................
Probe - Target Sequence 2
...............A..........
PROBE--5'TTTGCT.CACCCTTCCG3'
.........||||||.||||||||||
TARGET-3'AAACGA.GTGGGAAGGC5'
...............A..........
Probe - Target Sequence 3
...............T..........
PROBE--5'TTTGCT.CACCCTTCCG3'
.........||||||.||||||||||
TARGET-3'AAACGA.GTGGGAAGGC5'
...............T..........
Probe - Target Sequence 4
..........................
PROBE--5'TTTGCTTCACCCTTCCG3'
.........|||||||||||||||||
TARGET-3'AAACGAAGTGGGAAGGC5'
..........................
- The resulting formamide curves are shown below. The numbering follows the order of entry of the probe-target pairs. According to this output, the dissociation curves of GAM42a with its perfect match (curve 1) and mismatched (2) targets are too close for mismatch discrimination, while BET42a has a wider window of opportunity.
Figure 9. Formamide curves for GAM42a and BET42a hybridizing with E. coli and N. europaea 23S rRNA.

This tool evaluates mismatch stability with respect to free energy and formamide dissociation. The given is a probe, and perfect and mismatched targets to this probe. The output includes free energy values (ΔGo1, ΔGo2, ΔGo3, ΔGooverall), hybridization efficiency, and the formamide dissociation profiles for both targets, as well as the difference in these values created by the mismatch (except for ΔGo2, which does not change).
Input
-
Enter hybridization conditions: Temperature, Na+ concentration, and probe concentration.
-
Note: the probe concentration does not affect free energy values but affects hybridization efficiency and formamide curve.
-
-
Enter probe sequence from 5’ to 3’ end. mathFISH will align the probe with
each target to determine the best matching target site
on each organism.
-
Note: Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the probe sequence. For probes with degeneracy, evaluate the different combinations separately.
Enter target sequence information.
-
Select the target molecule.
- If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is. This is important for the calculation of ΔGo3.
-
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for the alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
Enter sequences for both the perfect match target and the non-target with mismatches (can use T instead of U; all T’s in target sequence will be converted to U’s) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Note: Degeneracy in target sequence (e.g. N, indicating all possibilities, i.e. A, C, G, or T) is treated as a mismatch at the probe target site. Other degeneracies in the target sequence are not allowed to base-pair, and this may affect the accuracy of ΔGo3 values.
Output
-
Probe-target site site alignment for both perfect match and mismatched sequences: This is a text output that shows the user how the probe aligns with the target site and how many mismatches there are.
-
Tabular
list of thermodynamic values: This list includes the free energy values (ΔGo1,
ΔGo2,
ΔGo3,
ΔGooverall),
hybridization efficiency,
and the melting formamide point ([FA]m).
-
Also included in the table is the difference in all values (Δvalue = value for mismatched target – value for perfect match target), which indicate the effect of mismatch insertion.
- The difference for ΔGo1 (ΔΔGo1) and [FA]m (Δ[FA]m) are highlighted since these are primary values used in the evaluation of mismatch stability (see Recommendations).
-
-
Graphical display of formamide dissociation profiles: This plot shows hybridization efficiency as a function of formamide concentration for both the target and non-target organism, thereby revealing the predicted effect of mismatches on the formamide dissociation. The difference between the curves is quantified by the Δ[FA]m value in the output table above.
-
The whole output can be downloaded as a report in text format.
Example
Take probe GAM42a, a probe that targets 23S rRNA of gammaproteobacteria. Take gammaproteobacterium E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695) as example perfect match target, and betaproteobacterium N. europaea ATCC 19718 (NC_004757) as the mismatched non-target. The objective is to compare the hybridization of GAM42a with E. coli and N. europaea.
Input:
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH), and probe concentration to 500nM (in the general range which is 250-1000nM).
-
Enter GAM42a sequence (“GCCTTCCCACATCGTTT”) in the probe sequence box.
-
Select target molecule as "Large Subunit rRNA" and domain of target organism as "Bacteria".
-
Enter target (E. coli) sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Enter non-target (N. europaea) sequence in a similar way. Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button.
Output:
-
The probe-target site alignment result is shown below. It indicates a perfect match alignment for the target organism and a single mismatch for the non-target.
Figure 10. Alignment of GAM42a with perfect match and one-mismatch target.
PROBE ALIGNMENT WITH TARGET ORGANISM:
..........................
PROBE--5'TTTGCTACACCCTTCCG3'
.........|||||||||||||||||
TARGET-3'AAACGATGTGGGAAGGC5'
..........................
PROBE ALIGNMENT WITH NON TARGET ORGANISM:
...............A..........
PROBE--5'TTTGCT.CACCCTTCCG3'
.........||||||.||||||||||
TARGET-3'AAACGA.GTGGGAAGGC5'
...............A..........
- The tabulated results are shown below. According to these results, ΔΔGo1 value is moderate and Δ[FA]m is too low for clear mismatch discrimination (see Recommendations).
Table 3. Thermodynamic descriptors of GAM42a hybridization with perfect match and one-mismatch targets.
|
|
TARGET ORGANISM |
NON-TARGET ORGANISM |
ΔValue |
|
ΔGo1 |
-21.0 kcal/mol |
-18.0 kcal/mol |
3.00 kcal/mol |
|
ΔGo2 |
1.5 kcal/mol |
1.5 kcal/mol |
NA |
|
ΔGo3 |
-5.5 kcal/mol |
-2.8 kcal/mol |
2.70 kcal/mol |
|
ΔGooverall |
-15.4 kcal/mol |
-15.2 kcal/mol |
0.20 kcal/mol |
|
[FA]m* |
37.6 % |
30.1 % |
-7.50 % |
|
Hybridization Efficiency** |
0.9999 |
0.9999 |
0.00 |
* Melting formamide concentration
** At 0% formamide
- The formamide dissociation curves are shown below. The plot indicates a narrow window for mismatch discrimination, as quantified by the Δ[FA]m value in the table.
Figure 11. Predicted formamide dissociation profiles of GAM42a with perfect match and one-mismatch targets

This tool evaluates the thermodynamics of probe hybridization with a target and a non-target organism, in the presence of a competitor oligonucleotide (Manz et al., 1992). The competitor is a perfect match to the non-target organism. Thus, it blocks probe hybridization site on the non-target, thereby reducing chances of cross hybridization.
The input includes four sequences: (1) probe, (2) competitor, (3) target organism (perfect match to probe), (4) non-target organism (perfect match to competitor). By the definition of FISH with competitor oligonucleotides, the probe must have mismatches to non-target and competitor to target. Otherwise, the algorithm places a warning sign, although calculations will be carried out. The output includes free energy values (ΔGo1, ΔGo2, ΔGo3, ΔGooverall), hybridization efficiency, and the formamide dissociation profiles for both targets for probe-target and probe-non-target hybridization.
Input
-
Enter hybridization conditions: Temperature, Na+ concentration, and probe concentration.
-
Note: the probe concentration does not affect free energy values but affects hybridization efficiency and formamide curves.
-
-
Enter probe and competitor sequence from 5’ to 3’ end. mathFISH will align both the probe and the competitor with each target sequence to determine the best matching target sites on each organism for both oligonucleotides. If the probe and competitor target sites do not match, a warning will appear in the results about the relative positioning of target sites.
-
Note: Degenerate nucleotides (e.g. W, indicating an A or T) are not allowed in the probe or competitor sequence. For probes with degeneracy, evaluate the different combinations separately.
Enter target sequence information.
-
Select the target molecule.
- If small or large subunit rRNA is selected, the sequence will first be aligned with the reference organism for the determination of the structural domain where the target site is. This is important for the calculation of ΔGo3.
-
-
If “Other” option is selected then no alignment will be done and the whole sequence will be used in ΔGo3 calculation.
-
Select the domain of life to which the target organism belongs. This dictates the reference organism for the alignment of the target molecule during ΔGo3 calculation. The reference organisms are Escherichia coli (Bacteria domain), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya).
-
Enter sequences for both the perfect match target and the non-target with mismatches (can use T instead of U; all T’s in target sequence will be converted to U’s) from 5’ to 3’. Acceptable formats include: plain sequence, Fasta, and GenBank (none case sensitive).
-
Note: Degeneracy in target sequence (e.g. N, indicating all possibilities, i.e. A, C, G, or T) is treated as a mismatch at the probe target site. Other degeneracies in the target sequence are not allowed to base-pair, and this may affect the accuracy of ΔGo3 values.
Output
-
Tabular list of thermodynamic values for all four combinations (in the absence of competition): probe-target, probe-non-target, competitor-target, and competitor-non-target hybridizations. This list includes the free energy values (ΔGo1, ΔGo2, ΔGo3, ΔGooverall) and hybridization efficiencyy.
-
Graphical display of formamide dissociation profiles: This plot shows hybridization efficiency of the probe as a function of formamide concentration for both the target and non-target organism, thereby revealing the predicted effect of competitor on the formamide dissociation.
-
The whole output can be downloaded as a report in text format.
Example
Take probe GAM42a, a probe that targets 23S rRNA of gammaproteobacteria. Take gammaproteobacterium E. coli O157:H7 str. Sakai (GenBank accession code: NC_002695) as the perfect match target, and betaproteobacterium N. europaea ATCC 19718 (NC_004757) as the mismatched non-target. The competitor designed for preventing GAM42a from binding to betaproteobacteria is “GCCTTCCCACTTCGTTT” (Manz et al., 1992), i.e., the perfect match to N. europaea for the same target site. Use this real example as the competitor. The objective is to compare the hybridization of GAM42a with E. coli and N. europaea when the competitor is used for preventing cross hybridization.
Input::
-
Use default temperature (T = 46oC) while changing [Na+] to 0.9M (generally used in FISH), and probe concentration to 500nM (in the general range which is 250-1000nM).
-
Enter GAM42a sequence (“GCCTTCCCACATCGTTT”) in the probe sequence box and competitor sequence (“GCCTTCCCACTTCGTTT”) in the competitor sequence box.
-
Select target molecule as "Large Subunit rRNA" and domain of target organism as "Bacteria".
-
Enter target (E. coli) sequence by copying and pasting (e.g., from a GenBank page or Bioedit interface). Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Enter non-target (N. europaea) sequence in a similar way. Click here to reach the example gene sequence in acceptable formats (plain text would also work).
-
Press SUBMIT button. ;
Output:
-
The tabulated results shown below indicate the hybridization of probe and competitor with the target and non-target sequences, when they are used alone (i.e., no competition). Thus, competitor has much higher affinity (i.e. more negative ΔGooverall) to non-target than the probe, which can potentially prevent cross hybridization. Likewise, the probe has higher affinity to the target than the competitor, lowering the chance of false negatives due to reduced probe sensitivity by competition. The implications for hybridization efficiency, when the probe and competitor are used together, can be visualized in the graphical output below.
Table 4. Thermodynamic descriptors of GAM42a and BET42a hybridization with target and non-target sequences defined by the user.
| Probe - Target | Probe - Non Target | Competitor - Target | Competitor - Non Target | |
| ΔGo1 kcal/mol | -20.97 | -18.01 | -18.15 | -21.37 |
| ΔGo2 kcal/mol | 1.54 | 1.54 | 1.54 | 1.54 |
| ΔGo3 kcal/mol | -5.47 | -2.79 | -5.47 | -2.79 |
| ΔGooverall kcal/mol | -15.44 | -15.16 | -12.63 | -18.52 |
| Hybridization Efficiency* | 1.0 | 1.0 | 1.0 | 1.0 |
*At 0% formamide
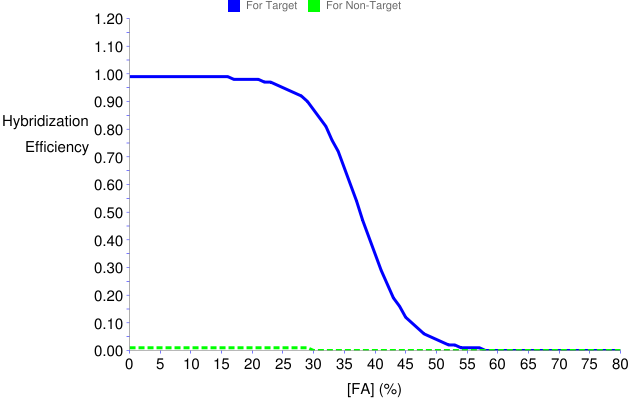
- The graphical output consists of the formamide dissociation curves shown below. Thus, as expected from the relative values in the table, cross hybridization with N. europaea is predicted to be insignificant throughout the formamide profile, and zeroed after 30% formamide (green dashed line), while probe sensitivity to E. coli is not significantly affected by the competition (i.e., plateau of blue solid line is close to 100% hybridization efficiency). See also recommendations for competitor analysis.
Figure 12. Predicted formamide dissociation profiles of GAM42a with perfect match and one-mismatch targets when BET42a is used as competitor
THERMODYNAMIC DESCRIPTIONS
This help document describes the thermodynamic terms used in the mathematical models of mathFISH. For each term, a short description and a summary of derivation are provided.
ΔG1o: Free Energy Change of Reaction 1
ΔG1o is the free energy change that defines the stability of DNA-RNA interactions between the probe and the target. In other words, it is the free energy change of hybridization assuming a linear probe structure and a fully accessible target site (i.e. both ΔG2o and ΔG3o are >>0, see below).
The derivation of ΔG1o follows different routes for perfect match and mismatched duplexes as explained below.
ΔG1o of Perfect Match Probe-Target Pairs
For perfect matches ΔG1o is calculated based on a nearest neighbor model using Equations 1-3 (Yilmaz and Noguera 2004), where H and S respectively denote enthalpy and entropy, n is the length of the probe, and the summation is over all n-1 nearest neighbors in the probe sequence. The nearest neighbor parameters are from Sugimoto et. al. (1995). Note that ΔG1o is a function of temperature (Equation 3) and salt strength ([Na+]; Equation 2), in addition to probe and target site sequences.
|
(1) |
|
|
(2) |
|
(3) |
ΔG1o of Mismatched Probe-Target Pairs and ΔΔG1o
Given a probe sequence, the relationship between ΔG1o with and without mismatches on the target site is described by:
|
|
(4) |
where, the first term on the right hand side is the perfect match ΔG1o as calculated based on nearest neighbors (see above) and the second term is the free energy penalty of mismatch insertion. Since DNA/RNA mismatch parameters are not complete, the second term is calculated according to a hybrid method proposed in Yilmaz et al. (2008).
According to this method, ΔΔG1o is first divided into two components as shown in Equation 5, where ΔΔG1o-NN represents the free energy loss due to the removal of nearest neighbor stackings upon mismatch insertion, and ΔΔG1o-loop indicates the stability of internal loops created by mismatches.
|
|
(5) |
To calculate ΔΔG1o, ΔΔG1o-NN is obtained from nearest neighbor rules for DNA/RNA interactions (Sugimoto et. al., 1995). The ΔΔG1o-loop value, on the other hand, is initially derived assuming DNA/DNA rules (hereafter designated as ΔΔG1o-loop,DNA/DNA'), and then RNA/RNA rules (ΔΔG1o-loop,RNA/RNA') for loop stability. In mathFISH, this derivation is conducted with UNAfold software (Markham and Zuker 2005, 2008), which can be manipulated to yield ΔG1o,mismatch, ΔG1o,perfect match, and ΔΔG1o-NN values for any probe-target site pair using DNA/DNA or RNA/RNA rules. Thus ΔΔG1o-loop,DNA/DNA' and ΔΔG1o-loop,RNA/RNA' can be obtained by plugging these values in Equations 4 and 5. Once DNA/DNA and RNA/RNA values are calculated, the ΔΔG1o-loop of the DNA/RNA hybridization is approximated by the average:
|
|
(6) |
Given the ΔΔG1o-loop value, ΔΔG1o is calculated using Equation 5, which is subsequently inserted in Equation 4 to obtain ΔG1o,mismatched at last.
ΔG2o: Free Energy Change of Reaction 2
ΔG2o is the free energy change that defines the stability of intramolecular DNA-DNA interactions within the probe. In other words, it is the free energy change of folding for the probe structure. The formation of this structure (Reaction 2) competes with probe-target duplex formation (Reaction 1).
ΔG2o is calculated by the UNAfold software (Markham and Zuker 2005, 2008), which gives free energy changes of possible structures for any DNA or RNA sequence. Probe sequence, temperature, and [Na+] are used as the input. Only the minimum free energy structure is found for these conditions, whose free energy defines ΔG2o (Yilmaz and Noguera, 2004).
ΔG3o is the free energy change that defines the stability of intramolecular secondary RNA-RNA interactions within the target molecule. In other words, it quantifies the accessibility of the target with respect to the secondary rRNA structure. Thus ΔG3o defines a free energy penalty working against the probe’s access to its target site.
ΔG3o is calculated using the UNAfold software (Markham and Zuker 2005, 2008), based on a method proposed by Yilmaz and Noguera, 2004. UNAfold software gives free energy changes of possible structures for any DNA or RNA sequence. For ΔG3o calculation, target sequence, position of probe target site in this sequence, and temperature are used as the input. Salt strength is fixed at the default value of [Na+] = 1M, since no salt correction is available for thermodynamic rules of RNA/RNA interactions. Thus ΔG3o calculations should be handled with care if [Na+] used in FISH experiments is significantly different than 1M.
If the target is small or large subunit rRNA, then the first step in ΔG3o calculation is the determination of the structural domain in which the target site resides (Yilmaz and Noguera, 2004). For small subunit rRNA, there are four domains that span residues 1-566, 567-912, 913-1396, and 1397-1542 in E. coli numbering. For large subunit rRNA, there are six domains that span residues 1-561, 562-1269, 1270-1646, 1647-2014, 2015-2625, and 2626-2904. To determine the domain of the target site, the whole target sequence is first aligned with a reference organism using ClustalW program (Thompson et al., 1994). The reference organisms are Escherichia coli (for the Bacterial domain of life; the domain of life is defined by the user), Methanosarcina barkeri (Archaea), and Saccharomyces cerevisiae (Eukarya). Then the structural domain of the target site is determined according to the positional alignment, and used in ΔG3o calculations, dismissing the rest of the target sequence. If the target site overlaps with two adjacent structural domains, then the combination of the two domains is used. If the target molecule is not either one of small or large subunit rRNA, then the alignment step is skipped and the whole sequence is used.
The partial sequence extracted by alignment (small or large subunit rRNA) or the whole sequence (other types of target molecules) is used as input for UNAfold to derive the free energy change of the formation of folded (ΔGRfo) and unfolded (ΔGRuo) structures in Reaction 3. To obtain ΔGRfo, target sequence is folded without any constraints. To obtain ΔGRuo, an array of specific constraints that ban base pairing at the target site are imposed on UNAfold. Finally, ΔG3o is calculated as the difference between folded and unfolded forms:
|
|
(7) |
ΔGoverallo: Overall Free Energy Change of Hybridization
ΔGooverall is the free energy change that defines the probability of probe-target hybridization at equilibrium, given the free energy changes of main (Reaction 1) and competing (Reactions 2 and 3) reactions. It is also called probe affinity (Yilmaz and Noguera, 2004).
Once individual reaction free energies (ΔGo1, ΔGo2, and ΔGo3) are calculated, the equilibrium constants of individual reactions are determined from Equation 8 (The forward direction of reactions is always taken towards the more structured state, i.e. up or right in the hybridization scheme). In this equation, R is the gas constant (0.00199 kcal/molK) and T designates the hybridization temperature in Kelvin.
|
|
(i = 1, 2, or 3) | (8) |
Using the reaction equilibrium constants, one can calculate the overall equilibrium constant for the hybridization scheme, which is defined by Equation 9, and expressed as a function of individual constants in Equation 10.
|
|
(9) |
|
|
(10) |
Finally, the overall standard Gibbs free energy change can be calculated from the fundamental relationship
|
|
(11) |
Hybridization Efficiency
Hybridization efficiency is defined as the theoretical ratio of probe-bound target molecules to all target molecules (i.e., [PR]/[Ro], where Ro represents total target). It can take values between 0 (no hybridization) and 1 (saturation). In the following, derivation of hybridization efficiency is described for regular FISH (single probes) and for the case when competitor oligonucleotides are used to enhance specificity.
Hybridization Efficiency for Single Probes
Hybridization efficiency is defined by Equation 12, which uses the conservation of mass for target (i.e., [Ro] = [PR]+[Ru]+[Rf]). Assuming excess probe over target ([Po] >> [Ro], where Po and Ro denote total probe and target, respectively), one can derive Equation 13 from Equation 12 (Yilmaz and Noguera, 2007). Thus, once Koverall is determined from free energy values, hybridization efficiency is calculated using Equation 13.
|
|
(12) |
|
|
(13) |
Hybridization Efficiency in the Presence of Competitor Oligonucleotides
Unlabeled competitor oligonucleotides (Manz et al. 1992) are often times employed in FISH to block target sites of non-target organisms with one or two mismatches to the probe, in order to minimize the chances of cross hybridization. The presence of a competitor greatly reduces the hybridization efficiency of the probe with the non-target (i.e. mismatched target molecule), while also affecting the hybridization with the perfect match. These effects can be simulated by thermodynamic modeling (Hoshino et al., 2008).
Given a target (or non-target) molecule, first the Koverall value is separately derived for the probe (Kpoverall) and competitor (KCoverall), using Equation 10. Then, the hybridization efficiency can be calculated for the probe according to:
|
|
(14) |
where Co denotes total competitor in hybridization buffer. The derivation of Equation 14 assumes [Po] >> [Ro] and [Co] >> [Ro] and uses a modified conservation of mass equation for the target: [Ro] = [CR]+[PR]+[Ru]+[Rf], where CR denotes competitor-target hybrid.
The term [Co]KCoverall in the denominator of Equation 14 determines the extent of the reduction in hybridization efficiency with respect to the normal case without a competitor (see Equation 13). Thus, for a non-target that perfectly matches the competitor but has mismatches to the probe, generally KCoverall >> KPoverall, and the hybridization efficiency can be radically reduced by this term provided a good design of competitor and probe. On the contrary, for a perfect match target, the design aims at KPoverall >> KCoverall so that the reduction in hybridization efficiency with the actual target does not drop significantly.
Formamide Dissociation Profiles
Theoretical formamide dissociation profiles show the decrease of hybridization efficiency with increasing formamide concentration in hybridization buffer. They are used as predictors of normalized experimental dissociation profiles, which show the decrease of probe-conferred signal intensity with increased formamide (Yilmaz and Noguera, 2007). In this section, the derivation of formamide dissociation profiles is presented. The special case with competitor oligonucleotides is also mentioned. In the end, two important variables regarding formamide denaturation are described.
Formamide Dissociation for Single Probes
Formamide denaturation is defined by a linear free energy model developed in Yilmaz and Noguera (2007). According to this model, the free energy values of individual reactions are calculated as a linear function of formamide:
|
|
(i = 1, 2, or 3) | (15) |
Thus, the free energy value at a given formamide concentration differs from that at zero formamide (i.e., the predicted value of ΔGo1, ΔGo2, and ΔGo3) by the multiplication of a slope, the m-value, and formamide concentration.
The m-values, which characterize the denaturing effect of formamide on each reaction, are defined by Equations 16-18 (Yilmaz and Noguera, 2007). Thus, m1 is expressed as a linear function of probe length (n), m3 as a linear function of ΔG3o, and m2 is approximated as a constant. It should be noted that m1 and m3 were calibrated using experimental data with E. coli (Yilmaz and Noguera, 2007), while the constant value of m2 is an educated approximation, which is consistent with microarray hybridization data with structured probes (Yilmaz et al, under preparation).
|
|
(16) |
|
|
(17) |
|
|
(18) |
Once free energy values are calculated for a given formamide concentration using Equation 15, they are plugged in Equation 8 to get equilibrium constants, which in turn yield the overall constant as a function of formamide concentration via Equation 10. Subsequently, the calculated Koverall value and the user-defined probe concentration are used to derive hybridization efficiency from Equation 13. When this procedure is repeated for an array of formamide concentrations, hybridization efficiency can be plotted as a function of formamide to derive the formamide dissociation profile.
Formamide Dissociation in the presence of Competitor Oligonucleotides
When a competitor oligonucleotide is present, the procedure above stays the same except that it is separately applied to both the probe and the competitor and Equation 14 replaces Equation 13 in the last step. For the use of theoretical formamide dissociation profiles in the presence of a competitor, see Hoshino et al. (2008).
[FA]m: Melting Formamide Concentration for the Probe-Target duplex
Theoretical formamide dissociation curves are generally sigmoid (an inverse S-shaped curve), as with most experimental trends. The midpoint of the sigmoid curve, i.e. the point where hybridization efficiency reaches a value of 0.5, is designated as the melting formamide concentration, [FA]m (Yilmaz et al., 2008). Thus, in theory, half of the target molecules are hybridized at the melting point.
Δ[FA]m: Difference in Melting Formamide Points
In general, the melting formamide concentraiton of a probe hybridizing with a mismatched target is less than that for the perfect match target. The difference, as defined by Equation 19 below, is an important indicator of mismatch stability (Yilmaz et al., 2008).
|
|
(19) |
RECOMMENDATIONS
This section provides a table of recommendations for the values of thermodynamic descriptors to be used in probe design. References are indicated when recommendations are based on published data. While these recommendations reflect the authors' current opinion of FISH probe design, users are encouraged to establish their own rules for an experience-based design approach and to provide feedback to the authors to improve the design criteria (a feedback upload page is available which can be accessed from the main page).
Table 1. Recommendations for probe design.
| Thermodynamic Variable | Recommendation | Reference |
| Hybridization Efficiency (HE) - Single Probes | A value of 1.0 (at no formamide condition) is recommended for maximizing sensitivity. To minimize specificity problems, ΔGooverall value should be considered additionally, i.e., the smallest range of about 3-4 kcal/mol ΔGooverall that gives HE = 1.0 should be targeted. See also ΔGooverall criteria below and the detailed recommendations based on mathFISH output. | Yilmaz and Noguera, 2004; Yilmaz et al., 2006 |
| ΔGooverall | The minimum range of about 3-4 kcal/mol ΔGooverall that gives an HE~1.0 (~100%) should be targeted. This corresponds to about -13 to -17 kcal/mol for typical probe concentration (250-1000nM). See also Hybridization Efficiency criteria above and the detailed recommendations based on mathFISH output. | Yilmaz and Noguera, 2004; Yilmaz et al., 2006 |
| ΔGo2 | An indicator of the stability of probe self-structure, largely negative values tend to reduce sensitivity even if HE and ΔGooverall criteria are satisfied (Yilmaz and Noguera, unpublished results). So, an arbitrary threshold of -3.0 is recommended for the decision process (i.e. more negative values should be avoided as much as possible). | n/a |
| [FA]m | Based on intuition, values larger than 55-60% are not recommended, as such high melting points would indicate very stable hybrids insensitive to mismatches, and therefore, mismatch discrimination ability would likely not be re-established even at high formamide values. | n/a |
| ΔΔGo1 | The larger the ΔΔGo1 value, the less the chance of cross hybridization with the non-target. With regard to mismatch discrimination potential, values can be regarded as poor (<2 kcal/mol), moderate (2-4 kcal/mol), and good (> 4 kcal/mol). Thus, introduction of competitor oligos to hybridization is strictly recommended for poor mismatch discrimination potential, and should be considered with care for moderate potential. | Yilmaz et al., 2008 |
| Δ[FA]m | Since -Δ[FA]m describes the width of the window of formamide concentrations that can potentially allow mismatch discrimination, absolute values less than 20% should be handled with care. Either competitor oligonucleotides should be used, or the precise value of the optimum formamide concentration for mismatch discrimination (if there is any)should be determined experimentally. | Yilmaz et al., 2008 |
| Hybridization Efficiency (HE) - with Competitor Oligos | When competitor oligonucleotides are used, the maximum achievable HE with perfect match target may be significantly less than 1.0. To avoid compromising sensitivity, we recommend that this value be maintained as greater than or equal to 0.9. Similarly, the maximum HE with the non-target should not be allowed to be greater than 0.1, to minimize the chance of false positives. | n/a |
REFERENCES
Hoshino, T., Yilmaz, L. S., Noguera, D. R., Daims, H., and Wagner, M. (2008) “Quantification of Target Molecules Needed to Detect Microorganisms by Fluorescence in situ Hybridization (FISH) and Catalyzed Reporter Deposition-FISH”, Applied and Environmental Microbiology, 74(16):5068-5077.
Manz W, et al. (1992). “Phylogenetic Oligodeoxynucleotide Probes for the Major Subclasses of Proteobacteria: Problems and Solutions” Systematic and Applied Microbiology 15:593-600.
Markham, N. R. & Zuker, M. (2005) “DINAMelt web server for nucleic acid melting prediction” Nucleic Acids Res., 33, W577-W581.
Markham, N. R. & Zuker, M. (2008) “UNAFold: software for nucleic acid folding and hybriziation” In Keith, J. M., editor, Bioinformatics, Volume II. Structure, Functions and Applications, number 453 in Methods in Molecular Biology, chapter 1, pages 3–31. Humana Press, Totowa, NJ. ISBN 978-1-60327-428-9.
Sugimoto, N.,et al. (1995) "Thermodynamic Parameters to Predict Stability of RNA/DNA Hybrid Duplexes" Biochemistry 34(35), 11211-11216.
Thompson JD, et al. (1994) “CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice” Nucleic Acids Res. 22:4673–4680.
Yilmaz, L. S. and Noguera, D. R. (2004) “Mechanistic Approach to the Problem of Hybridization Efficiency in Fluorescent in situ Hybridization”, Applied and Environmental Microbiology, 70: 7126-7139.
Yilmaz, L. S., Okten, H. E., and Noguera, D. R. (2006) “All Regions of the 16S rRNA of Escherichia coli are Accessible in situ to DNA Oligonucleotides with Sufficient Thermodynamic Affinity”, Applied and Environmental Microbiology, 72: 733-744.
Yilmaz, L. S. and Noguera, D. R. (2007) “Development of Thermodynamic Models for Simulating Probe Dissociation Profiles in Fluorescence in situ Hybridization”, Biotechnology and Bioengineering, 96 (2): 349-363.
Yilmaz, L. S., Bergsven, L., and Noguera, D. R. (2008) “Systematic Evaluation of Single Mismatch Stability Predictors for Fluorescence in situ Hybridization”, Environmental Microbiology, 10(10):2872-2085.
APPENDIX
E. coli 23S rRNA Sequence (ACC: NC_002695)
GenBank Format:
1 ggttaagcga ctaagcgtac acggtggatg ccctggcagt cagaggcgat gaaggacgtg
61 ctaatctgcg ataagcgtcg gtaaggtgat atgaaccgtt ataaccggcg atttccgaat
121 ggggaaaccc agtgtgattc gtcacactat cattaactga atccataggt taatgaggcg
181 aaccggggga actgaaacat ctaagtaccc cgaggaaaag aaatcaaccg agattccccc
241 agtagcggcg agcgaacggg gaggagccca gagcctgaat cagtgtgtgt gttagtggaa
301 gcgtctggaa aggcgcgcga tacagggtga cagccccgta cacaaaaatg cacatactgt
361 gagctcgatg agtagggcgg gacacgtggt atcctgtctg aatatggggg gaccatcctc
421 caaggctaaa tactcctgac tgaccgatag tgaaccagta ccgtgaggga aaggcgaaaa
481 gaaccccggc gaggggagtg aaaaagaacc tgaaaccgtg tacgtacaag cagtgggagc
541 ctcttttatg gggtgactgc gtaccttttg tataatgggt cagcgactta tattctgtag
601 caaggttaac cgaatagggg agccgaaggg aaaccgagtc ttaaccgggc gttaagttgc
661 agggtataga cccgaaaccc ggtgatctag ccatgggcag gttgaaggtt gggtaacact
721 aactggagga ccgaaccgac taatgttgaa aaattagcgg atgacttgtg gctgggggtg
781 aaaggccaat caaaccggga gatagctggt tctccccgaa agctatttag gtagcgcctc
841 gtgaattcat ctccgggggt agagcactgt ttcggcaagg gggtcatccc gacttaccaa
901 cccgatgcaa actgcgaata ccggagaatg ttatcacggg agacatacgg cgggtgctaa
961 cgtccgtcgt gaagagggaa acaacccaga ccgccagcta aggtcccaaa gtcatggtta
1021 agtgggaaac gatgtgggaa ggcccagaca gccaggatgt tggcttagaa gcagccatca
1081 tttaaagaaa gcgtaatagc tcactggtcg agtcggcctg cgcggaagat gtaacggggc
1141 taaaccatgc accgaagctg cggcagcgac actgtgtgtt gttgggtagg ggagcgttct
1201 gtaagcctgt gaaggtgtac tgtgaggtat gctggaggta tcagaagtgc gaatgctgac
1261 ataagtaacg ataaagcggg tgaaaagccc gctcgccgga agaccaaggg ttcctgtcca
1321 acgttaatcg gggcagggtg agtcgacccc taaggcgagg ccgaaaggcg tagtcgatgg
1381 gaaacaggtt aatattcctg tacttggtgt tactgcgaag gggggacgga gaaggctatg
1441 ttggccgggc gacggttgtc ccggtttaag cgtgtaggct ggttttccag gcaaatccgg
1501 aaaatcaagg ctgaggcgtg atgacgaggc actacggtgc tgaagcaaca aatgccctgc
1561 ttccaggaaa agcctctaag catcaggtaa catcaaatcg taccccaaac cgacacaggt
1621 ggtcaggtag agaataccaa ggcgcttgag agaactcggg tgaaggaact aggcaaaatg
1681 gtgccgtaac ttcgggagaa ggcacgctga tatgtaggtg aagtccctcg cggatggagc
1741 tgaaatcagt cgaagatacc agctggctgc aactgtttat taaaaacaca gcactgtgca
1801 aacacgaaag tggacgtata cggtgtgacg cctgcccggt gccggaaggt taattgatgg
1861 ggtcagcgca agcgaagctc ttgatcgaag ccccggtaaa cggcggccgt aactataacg
1921 gtcctaaggt agcgaaattc cttgtcgggt aagttccgac ctgcacgaat ggcgtaatga
1981 tggccaggct gtctccaccc gagactcagt gaaattgaac tcgctgtgaa gatgcagtgt
2041 acccgcggca agacggaaag accccgtgaa cctttactat agcttgacac tgaacattga
2101 gccttgatgt gtaggatagg tgggaggctt tgaagtgtgg acgccagtct gcatggagcc
2161 gaccttgaaa taccaccctt taatgtttga tgttctaacg tggacccgtg atccgggttg
2221 cggacagtgt ctggtgggta gtttgactgg ggcggtctcc tcctaaagag taacggagga
2281 gcacgaaggt tggctaatcc tggtcggaca tcaggaggtt agtgcaatgg cataagccag
2341 cttgactgcg agcgtgacgg cgcgagcagg tgcgaaagca ggtcatagtg atccggtggt
2401 tctgaatgga agggccatcg ctcaacggat aaaaggtact ccggggataa caggctgata
2461 ccgcccaaga gttcatatcg acggcggtgt ttggcacctc gatgtcggct catcacatcc
2521 tggggctgaa gtaggtccca agggtatggc tgttcgccat ttaaagtggt acgcgagctg
2581 ggtttagaac gtcgtgagac agttcggtcc ctatctgccg tgggcgctgg agaactgagg
2641 ggggctgctc ctagtacgag aggaccggag tggacgcatc actggtgttc gggttgtcat
2701 gccaatggca ctgcccggta gctaaatgcg gaagagataa gtgctgaaag catctaagca
2761 cgaaacttgc cccgagatga gttctccctg accctttaag ggtcctgaag gaacgttgaa
2821 gacgacgacg ttgataggcc gggtgtgtaa gcgcagcgat gcgttgagct aaccggtact
2881 aatgaaccgt gaggcttaac ctt
Fasta Format:
>gi|15829254:229090-231992 Escherichia coli O157:H7 str. Sakai, complete genome GGTTAAGCGACTAAGCGTACACGGTGGATGCCCTGGCAGTCAGAGGCGATGAAGGACGTGCTAATCTGCG ATAAGCGTCGGTAAGGTGATATGAACCGTTATAACCGGCGATTTCCGAATGGGGAAACCCAGTGTGATTC GTCACACTATCATTAACTGAATCCATAGGTTAATGAGGCGAACCGGGGGAACTGAAACATCTAAGTACCC CGAGGAAAAGAAATCAACCGAGATTCCCCCAGTAGCGGCGAGCGAACGGGGAGGAGCCCAGAGCCTGAAT CAGTGTGTGTGTTAGTGGAAGCGTCTGGAAAGGCGCGCGATACAGGGTGACAGCCCCGTACACAAAAATG CACATACTGTGAGCTCGATGAGTAGGGCGGGACACGTGGTATCCTGTCTGAATATGGGGGGACCATCCTC CAAGGCTAAATACTCCTGACTGACCGATAGTGAACCAGTACCGTGAGGGAAAGGCGAAAAGAACCCCGGC GAGGGGAGTGAAAAAGAACCTGAAACCGTGTACGTACAAGCAGTGGGAGCCTCTTTTATGGGGTGACTGC GTACCTTTTGTATAATGGGTCAGCGACTTATATTCTGTAGCAAGGTTAACCGAATAGGGGAGCCGAAGGG AAACCGAGTCTTAACCGGGCGTTAAGTTGCAGGGTATAGACCCGAAACCCGGTGATCTAGCCATGGGCAG GTTGAAGGTTGGGTAACACTAACTGGAGGACCGAACCGACTAATGTTGAAAAATTAGCGGATGACTTGTG GCTGGGGGTGAAAGGCCAATCAAACCGGGAGATAGCTGGTTCTCCCCGAAAGCTATTTAGGTAGCGCCTC GTGAATTCATCTCCGGGGGTAGAGCACTGTTTCGGCAAGGGGGTCATCCCGACTTACCAACCCGATGCAA ACTGCGAATACCGGAGAATGTTATCACGGGAGACATACGGCGGGTGCTAACGTCCGTCGTGAAGAGGGAA ACAACCCAGACCGCCAGCTAAGGTCCCAAAGTCATGGTTAAGTGGGAAACGATGTGGGAAGGCCCAGACA GCCAGGATGTTGGCTTAGAAGCAGCCATCATTTAAAGAAAGCGTAATAGCTCACTGGTCGAGTCGGCCTG CGCGGAAGATGTAACGGGGCTAAACCATGCACCGAAGCTGCGGCAGCGACACTGTGTGTTGTTGGGTAGG GGAGCGTTCTGTAAGCCTGTGAAGGTGTACTGTGAGGTATGCTGGAGGTATCAGAAGTGCGAATGCTGAC ATAAGTAACGATAAAGCGGGTGAAAAGCCCGCTCGCCGGAAGACCAAGGGTTCCTGTCCAACGTTAATCG GGGCAGGGTGAGTCGACCCCTAAGGCGAGGCCGAAAGGCGTAGTCGATGGGAAACAGGTTAATATTCCTG TACTTGGTGTTACTGCGAAGGGGGGACGGAGAAGGCTATGTTGGCCGGGCGACGGTTGTCCCGGTTTAAG CGTGTAGGCTGGTTTTCCAGGCAAATCCGGAAAATCAAGGCTGAGGCGTGATGACGAGGCACTACGGTGC TGAAGCAACAAATGCCCTGCTTCCAGGAAAAGCCTCTAAGCATCAGGTAACATCAAATCGTACCCCAAAC CGACACAGGTGGTCAGGTAGAGAATACCAAGGCGCTTGAGAGAACTCGGGTGAAGGAACTAGGCAAAATG GTGCCGTAACTTCGGGAGAAGGCACGCTGATATGTAGGTGAAGTCCCTCGCGGATGGAGCTGAAATCAGT CGAAGATACCAGCTGGCTGCAACTGTTTATTAAAAACACAGCACTGTGCAAACACGAAAGTGGACGTATA CGGTGTGACGCCTGCCCGGTGCCGGAAGGTTAATTGATGGGGTCAGCGCAAGCGAAGCTCTTGATCGAAG CCCCGGTAAACGGCGGCCGTAACTATAACGGTCCTAAGGTAGCGAAATTCCTTGTCGGGTAAGTTCCGAC CTGCACGAATGGCGTAATGATGGCCAGGCTGTCTCCACCCGAGACTCAGTGAAATTGAACTCGCTGTGAA GATGCAGTGTACCCGCGGCAAGACGGAAAGACCCCGTGAACCTTTACTATAGCTTGACACTGAACATTGA GCCTTGATGTGTAGGATAGGTGGGAGGCTTTGAAGTGTGGACGCCAGTCTGCATGGAGCCGACCTTGAAA TACCACCCTTTAATGTTTGATGTTCTAACGTGGACCCGTGATCCGGGTTGCGGACAGTGTCTGGTGGGTA GTTTGACTGGGGCGGTCTCCTCCTAAAGAGTAACGGAGGAGCACGAAGGTTGGCTAATCCTGGTCGGACA TCAGGAGGTTAGTGCAATGGCATAAGCCAGCTTGACTGCGAGCGTGACGGCGCGAGCAGGTGCGAAAGCA GGTCATAGTGATCCGGTGGTTCTGAATGGAAGGGCCATCGCTCAACGGATAAAAGGTACTCCGGGGATAA CAGGCTGATACCGCCCAAGAGTTCATATCGACGGCGGTGTTTGGCACCTCGATGTCGGCTCATCACATCC TGGGGCTGAAGTAGGTCCCAAGGGTATGGCTGTTCGCCATTTAAAGTGGTACGCGAGCTGGGTTTAGAAC GTCGTGAGACAGTTCGGTCCCTATCTGCCGTGGGCGCTGGAGAACTGAGGGGGGCTGCTCCTAGTACGAG AGGACCGGAGTGGACGCATCACTGGTGTTCGGGTTGTCATGCCAATGGCACTGCCCGGTAGCTAAATGCG GAAGAGATAAGTGCTGAAAGCATCTAAGCACGAAACTTGCCCCGAGATGAGTTCTCCCTGACCCTTTAAG GGTCCTGAAGGAACGTTGAAGACGACGACGTTGATAGGCCGGGTGTGTAAGCGCAGCGATGCGTTGAGCT AACCGGTACTAATGAACCGTGAGGCTTAACCTT
N. europaea 23S rRNA Sequence (ACC: NC_004757)
GenBank Format:
1 gatcaagtga ataagtgcat gtggtggatg ccttggcgat tacaggcgat gaaggacgtg
61 gaagcctgcg aaaagcttcg gggagctggc aaacaagctt tgatccggag atgtccgaat
121 gggaaaaccc acccgtaagg gtaatcactc ctgaatatat agggagatga tggctaacct
181 ggagaactga aacatctaag taaccagagg aaaagaaatc aacagagatt cccagagtag
241 tggcgagcga aatgggacca gcctgcagtt aataatattt agactaaccg aattatctgg
301 aaagttaaac cgtagtgggt gatagtcccg taggtgaaag tctgaatgtg gaactaagat
361 tgcaataagt agggcggggc acgtgtaatc ctgtctgaat atagggggac catcctctaa
421 ggctaaatac tcgtaatcga ccgatagtga accagtaccg tgagggaaag gcgaaaagaa
481 ccccgggagg ggagtgaaat agatcctgaa accgcatgca tacaaacagt aggagccttg
541 aaagaggtga ctgcgtacct tttgtataat gggtcagcga cttacattca gtagcgagct
601 taaccgatag gggaggcgta gtgaaaacga gtcttaatag ggcgataagt tgctgggtgt
661 agacccgaaa ccagatgatc tactcatggc caggatgaaa ggagggtaat gcctcgtgga
721 ggtccgaacc cactaatgtt gaaaaattag gggatgagct gtgggtaggg gtgaaaggct
781 aaacaaatct ggaaatagct ggttctctcc gaaaactatt taggtagtgc ctcatatatt
841 acctttgggg gtagagcact gttatggcta gggggtcgtc aagatttacc aaaccattgc
901 aaactccgaa taccaaagag tgcaagtatg ggagacagac atcgggtgct aacgttcggt
961 gtcgaaaggg aaacaaccca gaccttcagc taaggtccca aagatacagt taagtggtaa
1021 acgaagtggg aaggcataga cagtcaggaa gttggcttag aagcagccat cctttaaaga
1081 aagcgtaata gctcactgat cgagtcgtcc tgcgcggaag atgtaacggg gctaaactgt
1141 acaccgaagc taaggatttg caatttaatt gcaagtggta ggagagcgtt ccgtaagcct
1201 gtgaaggtaa cttgtgaagg ttgctggagg tatcggaagt gcgaatgctg acatgagtag
1261 cgataaagga agtgaaaagc ttcctcgccg aaaacccaag gtttcctgtg caacgttcat
1321 cggcgcaggg ttagtcggtc cctaaggtga ggtagaaata cgtagctgat gggaaactgg
1381 ttaatattcc agtaccttta tttaatgcga tgtggggacg aagaaggcta gcttagccgg
1441 gtgttggatg tcccggttga agcaggtaga catgctattt aggcaaatcc ggatagctta
1501 gtcgagatgt gataacgaaa cctctttcgg gaggccaagt aagtaatgcc atgcttccag
1561 gaaaagccac taagcttcag ttaaataaag accgtaccgt aaaccgacac aggtgggtgg
1621 gatgagaatt ctaaggcgct tgagagaact caggagaagg aactcggcaa attgacaccg
1681 taacttcggg agaaggtgtg cctctagtat gtgtagtgct acacgcatga agcagaatga
1741 ggttgcaaag aaatggtggc tgcgactgtt taataaaaac acagcactct gcaaacacga
1801 aagtggacgt atagggtgtg acgcctgccc ggtgccggaa ggttaagtga tggggtgcaa
1861 gctcttgatc gaagccccgg taaacggcgg ccgtaactat aacggtccta aggtagcgaa
1921 attccttgtc gggtaagttc cgacctgcac gaatggcgta acgatggcca cactgtctcc
1981 tcctgagact cagcgaagtt gaaatgtttg tgaagatgca atctacccgc ggctagacgg
2041 aaagaccccg tgcaccttta ctgtagcttt acattggatt ttgattattc ttgtgtagga
2101 taggtgggag gctgtgaaat atgctcgcca gagtgtatgg agccaacctt gaaataccac
2161 cctggaatga tcggagttct aacccaggtc cattatctgg atcggggacc gtgtatggta
2221 ggcagtttga ctggggcggt ctcctcccaa agagtaacgg aggagtgcga aggtacgcta
2281 ggtacggtcg gaaatcgtac tgatagtgca atggcataag cgtgcttaac tgcgagactg
2341 acaagtcgag cagatgcgaa agcaggtcat agtgatccgg tggttctgta tggaagggcc
2401 atcgctcaac ggataaaagg tacgccgggg ataacaggct gattcctccc aagagttcat
2461 atcgacgggg gagtttggca cctcgatgtc ggctcatcac atcctggggc tgtagtcggt
2521 cccaagggta tggctgttcg ccatttaaag tggtacgtga gctgggttta aaacgtcgtg
2581 agacagtttg gtccctatct gccgtgggcg ttggaaattt gagtggggct gctcctagta
2641 cgagaggacc ggagtggacg cacctctggt gtaccggtta tgacgccagt cgtatcgccg
2701 ggtagctaag tgcggaagag ataaccgctg aaagcatcta agcgggaaac ttgccataag
2761 attagatttc ccgggaattt aattccccta aaggttcgtt gaagactaca acgttgatag
2821 gtcgaatgtg taagcgtagt aatgcgttaa gctaatcgat actaattgac cgtgaggctt
2881 gatcct
Fasta Format:
>gi|30248031:71083-73968 Nitrosomonas europaea ATCC 19718, complete genome GATCAAGTGAATAAGTGCATGTGGTGGATGCCTTGGCGATTACAGGCGATGAAGGACGTGGAAGCCTGCG AAAAGCTTCGGGGAGCTGGCAAACAAGCTTTGATCCGGAGATGTCCGAATGGGAAAACCCACCCGTAAGG GTAATCACTCCTGAATATATAGGGAGATGATGGCTAACCTGGAGAACTGAAACATCTAAGTAACCAGAGG AAAAGAAATCAACAGAGATTCCCAGAGTAGTGGCGAGCGAAATGGGACCAGCCTGCAGTTAATAATATTT AGACTAACCGAATTATCTGGAAAGTTAAACCGTAGTGGGTGATAGTCCCGTAGGTGAAAGTCTGAATGTG GAACTAAGATTGCAATAAGTAGGGCGGGGCACGTGTAATCCTGTCTGAATATAGGGGGACCATCCTCTAA GGCTAAATACTCGTAATCGACCGATAGTGAACCAGTACCGTGAGGGAAAGGCGAAAAGAACCCCGGGAGG GGAGTGAAATAGATCCTGAAACCGCATGCATACAAACAGTAGGAGCCTTGAAAGAGGTGACTGCGTACCT TTTGTATAATGGGTCAGCGACTTACATTCAGTAGCGAGCTTAACCGATAGGGGAGGCGTAGTGAAAACGA GTCTTAATAGGGCGATAAGTTGCTGGGTGTAGACCCGAAACCAGATGATCTACTCATGGCCAGGATGAAA GGAGGGTAATGCCTCGTGGAGGTCCGAACCCACTAATGTTGAAAAATTAGGGGATGAGCTGTGGGTAGGG GTGAAAGGCTAAACAAATCTGGAAATAGCTGGTTCTCTCCGAAAACTATTTAGGTAGTGCCTCATATATT ACCTTTGGGGGTAGAGCACTGTTATGGCTAGGGGGTCGTCAAGATTTACCAAACCATTGCAAACTCCGAA TACCAAAGAGTGCAAGTATGGGAGACAGACATCGGGTGCTAACGTTCGGTGTCGAAAGGGAAACAACCCA GACCTTCAGCTAAGGTCCCAAAGATACAGTTAAGTGGTAAACGAAGTGGGAAGGCATAGACAGTCAGGAA GTTGGCTTAGAAGCAGCCATCCTTTAAAGAAAGCGTAATAGCTCACTGATCGAGTCGTCCTGCGCGGAAG ATGTAACGGGGCTAAACTGTACACCGAAGCTAAGGATTTGCAATTTAATTGCAAGTGGTAGGAGAGCGTT CCGTAAGCCTGTGAAGGTAACTTGTGAAGGTTGCTGGAGGTATCGGAAGTGCGAATGCTGACATGAGTAG CGATAAAGGAAGTGAAAAGCTTCCTCGCCGAAAACCCAAGGTTTCCTGTGCAACGTTCATCGGCGCAGGG TTAGTCGGTCCCTAAGGTGAGGTAGAAATACGTAGCTGATGGGAAACTGGTTAATATTCCAGTACCTTTA TTTAATGCGATGTGGGGACGAAGAAGGCTAGCTTAGCCGGGTGTTGGATGTCCCGGTTGAAGCAGGTAGA CATGCTATTTAGGCAAATCCGGATAGCTTAGTCGAGATGTGATAACGAAACCTCTTTCGGGAGGCCAAGT AAGTAATGCCATGCTTCCAGGAAAAGCCACTAAGCTTCAGTTAAATAAAGACCGTACCGTAAACCGACAC AGGTGGGTGGGATGAGAATTCTAAGGCGCTTGAGAGAACTCAGGAGAAGGAACTCGGCAAATTGACACCG TAACTTCGGGAGAAGGTGTGCCTCTAGTATGTGTAGTGCTACACGCATGAAGCAGAATGAGGTTGCAAAG AAATGGTGGCTGCGACTGTTTAATAAAAACACAGCACTCTGCAAACACGAAAGTGGACGTATAGGGTGTG ACGCCTGCCCGGTGCCGGAAGGTTAAGTGATGGGGTGCAAGCTCTTGATCGAAGCCCCGGTAAACGGCGG CCGTAACTATAACGGTCCTAAGGTAGCGAAATTCCTTGTCGGGTAAGTTCCGACCTGCACGAATGGCGTA ACGATGGCCACACTGTCTCCTCCTGAGACTCAGCGAAGTTGAAATGTTTGTGAAGATGCAATCTACCCGC GGCTAGACGGAAAGACCCCGTGCACCTTTACTGTAGCTTTACATTGGATTTTGATTATTCTTGTGTAGGA TAGGTGGGAGGCTGTGAAATATGCTCGCCAGAGTGTATGGAGCCAACCTTGAAATACCACCCTGGAATGA TCGGAGTTCTAACCCAGGTCCATTATCTGGATCGGGGACCGTGTATGGTAGGCAGTTTGACTGGGGCGGT CTCCTCCCAAAGAGTAACGGAGGAGTGCGAAGGTACGCTAGGTACGGTCGGAAATCGTACTGATAGTGCA ATGGCATAAGCGTGCTTAACTGCGAGACTGACAAGTCGAGCAGATGCGAAAGCAGGTCATAGTGATCCGG TGGTTCTGTATGGAAGGGCCATCGCTCAACGGATAAAAGGTACGCCGGGGATAACAGGCTGATTCCTCCC AAGAGTTCATATCGACGGGGGAGTTTGGCACCTCGATGTCGGCTCATCACATCCTGGGGCTGTAGTCGGT CCCAAGGGTATGGCTGTTCGCCATTTAAAGTGGTACGTGAGCTGGGTTTAAAACGTCGTGAGACAGTTTG GTCCCTATCTGCCGTGGGCGTTGGAAATTTGAGTGGGGCTGCTCCTAGTACGAGAGGACCGGAGTGGACG CACCTCTGGTGTACCGGTTATGACGCCAGTCGTATCGCCGGGTAGCTAAGTGCGGAAGAGATAACCGCTG AAAGCATCTAAGCGGGAAACTTGCCATAAGATTAGATTTCCCGGGAATTTAATTCCCCTAAAGGTTCGTT GAAGACTACAACGTTGATAGGTCGAATGTGTAAGCGTAGTAATGCGTTAAGCTAATCGATACTAATTGAC CGTGAGGCTTGATCCT